Notes for Lecture 6

---

Recursion

---

定义

递归是指一种算法在某种程度上以较小的形式引用它自己

引入

递归程序设计

自相似

练习

阶乘

int factorial(int n) {

	if (n == 1 || n == 0) {
		return 1;
	}
	else {
		return n * factorial(n - 1);
	}

}

回文判断

bool plalindrome(string n) {

	if (n.length() <= 0) {
		return true;
	}else{
		char start = n[0];
		char end = n[n.length() - 1];
		string sub = n.substr(1, n.length() - 2);
		if (start != end) {
			return false;
		}else{
			return plalindrome(sub);
		}
		//return start == end && plalindrome(sub);
	}

}

汉诺塔分治递归

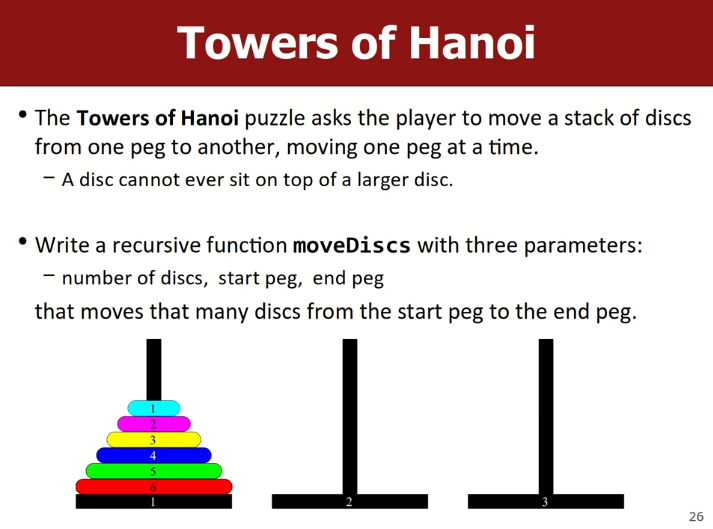
void Hanoi(int n, string a, string b, string c){
	static int num = 0;
	if (n <= 0)
	{
		return;
	}
	else {
		Hanoi(n - 1, a, c, b);
		cout << "第" << ++num << "次移动" << n << "号盘" << a << "->" << c << endl;
		Hanoi(n - 1, b, a, c);
	}
}

递归与分治策略

原文链接：https://blog.csdn.net/zhongkelee/article/details/45485943

分治的基本过程

• Divide：将问题的规模变小,直到问题规模足够小，很容易求出其解为止

• 分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。原问题与子问题的唯一区别是输入规模不同。

• 分解的要点：
  a.分解的条件要互斥；
  b.分解后的所有结果加在一起，能够覆盖原始问题的所有情况。

• Conquer：递归的处理小规模问题（只需递归调用即可）
• Combine：将小规模问题的解合并为原始问题的解

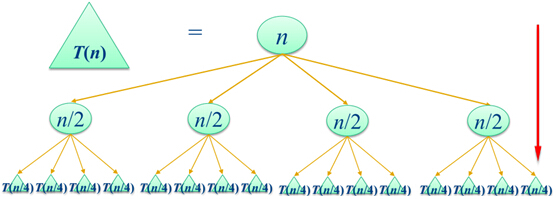
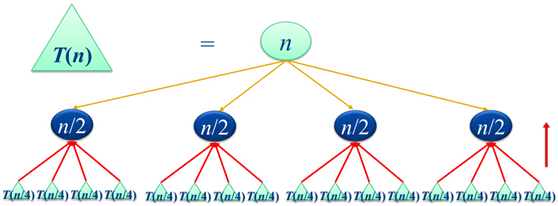
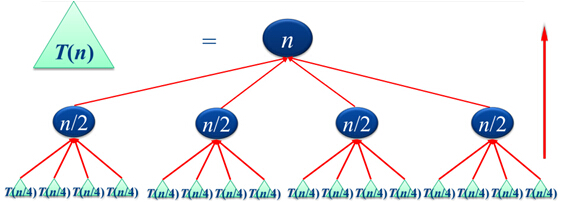
实例

二分搜索技术

-分析
无论是在前面还是后面查找x，其方法都和在a中查找x一样，只不过是查找的规模缩小了，很显然此问题分解出的子问题相互独立，即在排好序数组的前面或后面查找x是独立的子问题，因此满足分治法的适用条件。

int BinarySearch(int arr[], int x, int left, int right){
    while(left <= right){
        int middle = (left + right)/2;
        if (arr[middle] == x)
            return middle;
        if (arr[middle] > x)
            right = middle - 1;
        else
            left = middle + 1;
    }
    return -1;
}